The Electric Field Around a Charged Spherical Shell
Background
Hello again! It has been a while, but I am back and blogging. Over the next few weeks, you are going to see some big changes to the layout and organization of the site as I add a personal touch to all of the blog posts. I will keep you posted on the updates as they come.
But for now, let’s get back into physics! In introductory physics, we often give students example problems with the expectation that they will solve them using a specific method. Very rarely do we revisit a problem and show that it can be solved in a number of ways. Today, I want to talk about the thin, charged spherical shell and show that one can use Coulomb’s law rather than the traditional method of Gauss’s law to solve it.
Suppose I have a charged spherical shell with radius \(R\) and total charge +Q. This shell will have no thickness, so all of the charge +Q is uniformly distributed over the surface area of the shell. I want to determine the electric field some distance \(r\) away from the center of my sphere where \(r > R\).
We know from Gauss’s law that the electric field outside of the shell should be similar to that of a point charge:
\[\begin{equation} \vec{E} = \frac{kQ}{r^2} \hat{r} \end{equation}\]How would we go through this problem if we wanted to use Coulomb’s law rather than Gauss’s law? We ought to get the same answer no matter what method we choose.
Let’s begin by cutting up the surface of the shell into many tiny pieces, each with a tiny area \(dA\) and a tiny charge \(dq\).
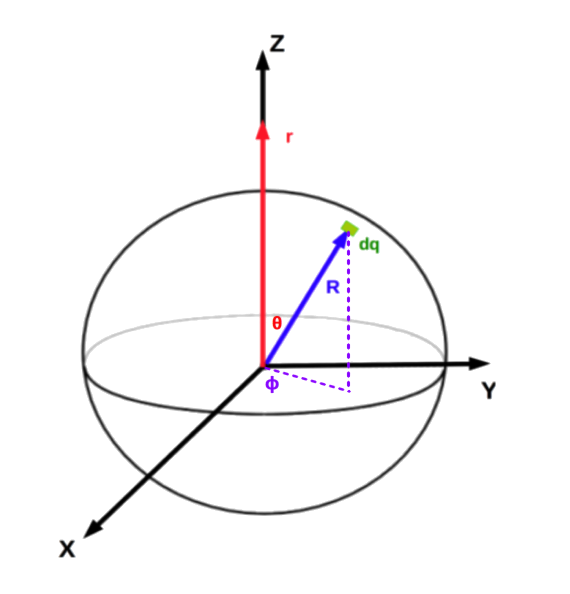
We know that the tiny charge is simply equal to the charge density (charge per unit area) times the tiny area:
\[\begin{equation} dq = \sigma dA = \left ( \frac{+Q}{4\pi R^2} \right ) \left ( R^2 sin\theta d\theta d\phi \right ) = \frac{Q sin\theta d\theta d\phi}{4\pi} \end{equation}\]Note that the tiny area \(dA\) is simply a solid angle multiplied by the radius of the sphere squared. There is no \(dr\) term in the expression above because the charged shell has no thickness.
If we take a slice of the sphere as shown below, we can define a few quantities that will help us in our analysis.
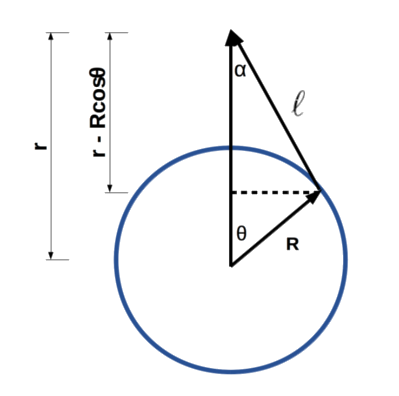
Using the law of cosines, we get:
\[\begin{equation} \ell^2 = r^2 + R^2 -2rRcos\theta \end{equation}\]And from trigonometry, we get:
\[\begin{equation} cos\alpha = \frac{r - Rcos\theta}{\ell} \end{equation}\]We can put all of this together to solve for the electric field:
\[\begin{align} \vec{dE} &= \frac{k dq}{\ell^2} \hat{\ell}\\[0.1cm] &= \frac{k \left (\frac{Q sin\theta d\theta d\phi}{4\pi} \right )}{\ell^2} \hat{\ell}\\[0.1cm] &= \frac{kQ sin\theta d\theta d\phi}{4 \pi \ell^2} \hat{\ell}\\[0.1cm] \end{align}\]Looking at the diagram above, we need to take into acccount the direction of the final electric field vector. Although each tiny electric field \(\vec{dE}\) will point in a different direction, the total electric field \(\vec{E}\) will point directly along the z-axis because all of the components of \(\vec{E}\) along the x- or y-axis will cancel.
\[\begin{equation} \vec{dE}_z = \frac{kQ sin\theta d\theta d\phi}{4 \pi \ell^2} (cos\alpha) \hat{z} \end{equation}\]We can now integrate over \(\theta\) and \(\phi\):
\[\begin{align} \vec{E} &= \int_0^{2\pi} \int_0^\pi \frac{kQ sin\theta d\theta d\phi}{4 \pi \ell^2} (cos\alpha) \hat{z}\\[0.1cm] &= \frac{kQ}{4\pi} \int_0^{2\pi} \int_0^\pi \left ( \frac{sin\theta d\theta d\phi}{\ell^2} \right ) \left (\frac{r - Rcos\theta}{\ell} \right )\hat{z}\\[0.1cm] &= \frac{kQ}{4\pi} \int_0^{2\pi} \int_0^\pi \frac{sin\theta (r - Rcos\theta) d\theta d\phi}{\ell^3} \hat{z}\\[0.1cm] &= \frac{kQ}{4\pi} \int_0^{2\pi} \int_0^\pi \frac{sin\theta (r - Rcos\theta) d\theta d\phi}{(r^2 + R^2 - 2rRcos\theta)^{3/2}} \hat{z} \end{align}\]The integral over \(d\phi\) simply yields \(2\pi\):
\[\begin{equation} \vec{E} = \frac{kQ}{2} \int_0^\pi \frac{sin\theta (r - Rcos\theta) d\theta}{(r^2 + R^2 - 2rRcos\theta)^{3/2}} \hat{z} \end{equation}\]We can simplify this integral using u-substitution. Let \(u = cos\theta\) and \(du = -sin\theta d\theta\). Then:
\[\begin{align} \vec{E} &= \frac{kQ}{2} \int_1^{-1} \frac{- (r - Ru) du}{(r^2 + R^2 - 2rRu)^{3/2}} \hat{z}\\[0.1cm] &= \frac{kQ}{2} \int_{-1}^1 \frac{(r - Ru) du}{(r^2 + R^2 - 2rRu)^{3/2}} \hat{z} \end{align}\]I decided to use an integral table here:
\[\begin{align} \vec{E} &= \frac{kQ}{2} \left [ \frac{ru - R}{r^2 \sqrt{r^2 + R^2 - 2rRu}} \right ]_{-1}^1 \hspace{2mm} \hat{z}\\[0.1cm] &= \frac{kQ}{2} \left [ \frac{r - R}{r^2 \sqrt{r^2 + R^2 - 2rR}} + \frac{r + R}{r^2 \sqrt{r^2 + R^2 + 2rR}} \right ] \hat{z} \\[0.1cm] &= \frac{kQ}{2r^2} \left [ \frac{r - R}{\sqrt{r^2 + R^2 - 2rR}} + \frac{r + R}{\sqrt{r^2 + R^2 + 2rR}} \right ] \hat{z} \\[0.1cm] &= \frac{kQ}{2r^2} \left [ \frac{r - R}{\sqrt{(r-R)^2}} + \frac{r + R}{\sqrt{(r+R)^2}} \right ] \hat{z}\\[0.1cm] &= \frac{kQ}{2r^2} \left [ \frac{r - R}{r - R} + \frac{r + R}{r + R} \right ] \hat{z}\\[0.1cm] &= \frac{kQ}{2r^2} \left [ 1 + 1 \right ] \hat{z}\\[0.1cm] &= \frac{2kQ}{2r^2} \hat{z}\\[0.1cm] &= \frac{kQ}{r^2} \hat{z}\\[0.1cm] \end{align}\]We get the same answer no matter what method we use.