Maximum Range of a Projectile
Introduction
Source Code: https://github.com/CupcakePhysics/projectile_range/releases/tag/v1.0.0
In introductory mechanics courses, we learn that we need to launch a projectile at an angle of \(45^\circ\) for maximum range. However, this derivation only works when we are studying the kinematics of a projectile on flat ground. What would happen if we launched the projectile off of a cliff? Does the maximum range still correspond to \(45^\circ\)? Does it depend on the height of the cliff?
Range on Flat Surface
Let’s review the derivation of the maximum range of a projectile (neglecting air resistance). Consider the setup shown below.
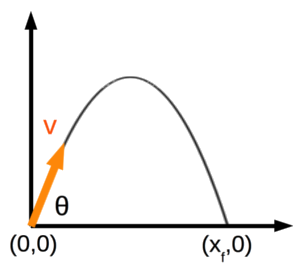
We launch a projectile with an initial speed \(v\) at an angle \(\theta\) with respect to the horizontal axis. It makes a parabolic arc through the air due to the acceleration due to gravity (\(g\)) and then lands some distance \(x_f\) away. I will use the kinematics equations to analyze this problem.
First, we can solve for the time of flight by analyzing motion in the vertical (y) direction.
\[\begin{align} y_f &= y_i + v_{iy} t + \frac{1}{2} a_y t^2\\[0.1cm] 0 &= 0 + v sin\theta t - \frac{1}{2} g t^2 \end{align}\]Solving for the time \(t\) yields:
\[\begin{align} v sin\theta t &= \frac{1}{2} g t^2\\[0.1cm] v sin\theta &= \frac{1}{2} g t\\[0.1cm] \frac{2 v sin\theta}{g} &= t\\[0.1cm] \end{align}\]Next, we can analyze the motion along the horizontal (x) direction.
\[\begin{align} x_f &= x_i + v_{ix} t + \frac{1}{2} a_x t^2\\[0.1cm] x_f &= 0 + v cos\theta t + 0\\[0.1cm] x_f &= v cos\theta t \end{align}\]Substituting the expression for \(t\) into the expression for \(x_f\) yields:
\[\begin{align} x_f &= v cos\theta t\\[0.1cm] x_f &= \frac{2 v^2 cos\theta sin\theta}{g}\\[0.1cm] \end{align}\]If we want to find the maximum range of the projectile, we take the derivative of \(x_f\) with respect to \(\theta\) and set it equal to zero:
\[\begin{align} \frac{d x_f}{d\theta} &= \frac{2 v^2}{g} \frac{d}{d\theta} \left [ cos\theta sin\theta \right ]\\[0.1cm] &= \frac{2 v^2}{g} \left [ cos^2 \theta - sin^2\theta \right ]\\[0.1cm] &= \frac{2 v^2}{g} cos\left ( 2\theta \right ) \end{align}\] \[\begin{align} 0 &= \frac{2 v^2}{g} cos\left ( 2\theta \right )\\[0.1cm] 0 &= cos\left ( 2\theta \right )\\[0.1cm] \theta &= 45^\circ \end{align}\]As we expect, the maximum range of the projectile occurs when \(\theta = 45^\circ\).
Range Off Cliff
Now suppose that instead of a flat surface we launch the projectile off of a cliff as shown below.
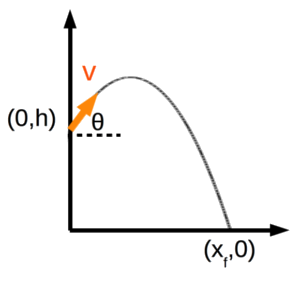
Everything is the same as before, except now, the starting position is (0,h) rather than (0,0). At what angle do we see a maximum?
We can start our analysis just like before. First, we will analyze the motion along the vertical (y) direction. This time, the initial y position \(y_i\) does not equal zero.
\[\begin{align} y_f &= y_i + v_{iy} t + \frac{1}{2} a_y t^2\\[0.1cm] 0 &= h + v sin\theta t - \frac{1}{2} g t^2\\[0.1cm] 0 &= g t^2 - 2v sin\theta t - 2h\\[0.1cm] \end{align}\]Solving for t using the quadratic formula yields:
\[\begin{align} t &= \frac{2vsin\theta \pm \sqrt{4v^2 sin^2\theta - 4g(-2h)}}{2g}\\[0.1cm] &= \frac{2vsin\theta \pm \sqrt{4v^2 sin^2\theta + 8gh}}{2g}\\[0.1cm] &= \frac{vsin\theta}{g} \pm \frac{\sqrt{v^2 sin^2\theta + 2gh}}{g}\\[0.1cm] \end{align}\]We note that the minus solution will give us a negative time. This is not a physically real solution, so we will only focus on the positive one.
\[\begin{equation} t = \frac{vsin\theta}{g} + \frac{\sqrt{v^2 sin^2\theta + 2gh}}{g} \end{equation}\]Now, once again we can analyze the motion in the horizontal (x) direction. Solving for \(x_f\) yields:
\[\begin{align} x_f &= x_i + v_{ix} t + \frac{1}{2} a_x t^2\\[0.1cm] x_f &= 0 + v cos\theta t + 0\\[0.1cm] x_f &= v cos\theta t \end{align}\]Substituting in the expression for \(t\) into the expression for \(x_f\) yields:
\[\begin{align} x_f &= v cos\theta t\\[0.1cm] &= v cos\theta \left [ \frac{vsin\theta}{g} + \frac{\sqrt{v^2 sin^2\theta + 2gh}}{g} \right ]\\[0.1cm] &= \frac{v^2 cos\theta sin\theta}{g} + \frac{v cos\theta \sqrt{v^2 sin^2\theta + 2gh}}{g}\\[0.1cm] \end{align}\]That looks a lot more complicated than the expression we got in the case of flat ground…
We could proceed as we did above, taking the derivative and setting it equal to zero. However, I really wouldn’t recommend it. The derivative itself is messy, but doable:
\[\begin{align} \frac{d x_f}{d\theta} &= \frac{v^2}{g}\frac{d}{d\theta}\left [ cos\theta sin\theta \right ] + \frac{v}{g} \frac{d}{d\theta} \left [ cos\theta \sqrt{v^2 sin^2\theta + 2gh} \right ]\\[0.1cm] &= \frac{v^2}{g} \left [ cos^2\theta - sin^2\theta \right ] + \frac{v}{g} \left [ cos\theta \left (v^2 sin^2\theta + 2gh\right )^{-1/2} \left ( 2 v^2 sin\theta cos\theta \right ) - sin\theta \sqrt{v^2 sin^2\theta + 2gh} \right ]\\[0.1cm] &= \frac{v^2}{g} cos \left (2\theta \right) + \frac{v}{g} \left [ \frac{ 2 v^2 sin\theta cos^2\theta}{\sqrt{v^2 sin^2\theta + 2gh}} - \frac{ sin\theta \left (v^2 sin^2\theta + 2gh \right )}{\sqrt{v^2 sin^2\theta + 2gh}} \right ]\\[0.1cm] &= \frac{v^2}{g} cos \left (2\theta \right) + \frac{v}{g} \left [ \frac{ 2 v^2 sin\theta cos^2\theta}{\sqrt{v^2 sin^2\theta + 2gh}} - \frac{ v^2 sin^3\theta + 2gh sin\theta}{\sqrt{v^2 sin^2\theta + 2gh}} \right ]\\[0.1cm] &= \frac{v^2}{g} cos \left (2\theta \right) + \frac{v}{g} \left [ \frac{ 2 v^2 sin\theta cos^2\theta - v^2 sin^3\theta + 2gh sin\theta}{\sqrt{v^2 sin^2\theta + 2gh}} \right ]\\[0.1cm] &= \frac{v^2}{g} cos \left (2\theta \right) + \frac{v sin\theta}{g} \left [ \frac{ 2 v^2 cos^2\theta - v^2 sin^2\theta + 2gh}{\sqrt{v^2 sin^2\theta + 2gh}} \right ]\\[0.1cm] \end{align}\]But solving the final equation for \(\theta\) is a nightmare:
\[\begin{equation} 0 = \frac{v^2}{g} cos \left (2\theta \right) + \frac{v sin\theta}{g} \left [ \frac{ 2 v^2 cos^2\theta - v^2 sin^2\theta + 2gh}{\sqrt{v^2 sin^2\theta + 2gh}} \right ] \hspace{7mm} :( \end{equation}\]Don’t believe me? Here is the solution in Wolfram Alpha. If you have a Wolfram account, feel free to run the problem with more computing time and see what you get!
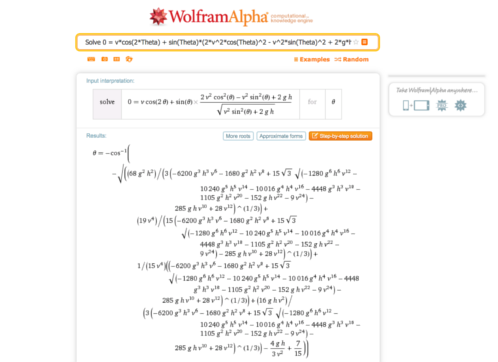
Oh god, kill it with fire…
Instead of struggling with the analytical solution, maybe we can look at this problem numerically. I have written a little Matlab script that plots the range of the projectile as a function of angle. You can customize the starting height of the projectile in the parameters at the top of the script. Feel free to play around with it.
An example output is shown below. Here, I have plotted heights of:
- h1 = 0 m
- h2 = 2 m
- h3 = 4 m
- h4 = 6 m
- h5 = 8 m.
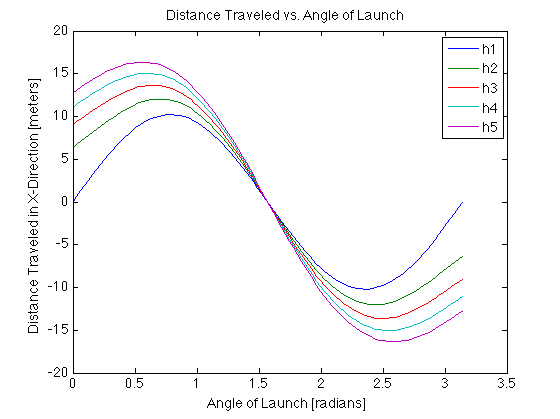
Notice that the distance traveled is negative when the angle is greater than \(\pi/2\) radians. This is because we are effectively launching the projectile “backwards”. In any case, we see that as the height increases, the maximum range increases as well. Additionally, as the height increases, the maximum range occurs at smaller and smaller angles.
Thus, we finally get to our result. If we are on a flat surface, the angle of maximum range is \(45^\circ\). However, as we increase the initial height (h) of the projectile, we need to throw it at a shallower angle in order to get maximum distance (less than \(45^\circ\)).